Whenever I give an interview with a good company, this question always comes up, sometimes straight, sometimes molded.

Why do we have to use it? The main work in the interview is to reduce the time complexity of the given solution you give, sliding window will never be the first solution you will tell the interviewer, sliding window is the way to reduce the running of a multiloop and remove it with a single one, thereby reducing the time complexity.

Let's learn this using a LeetCode Question,

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

Return the maximum sum from all windows.

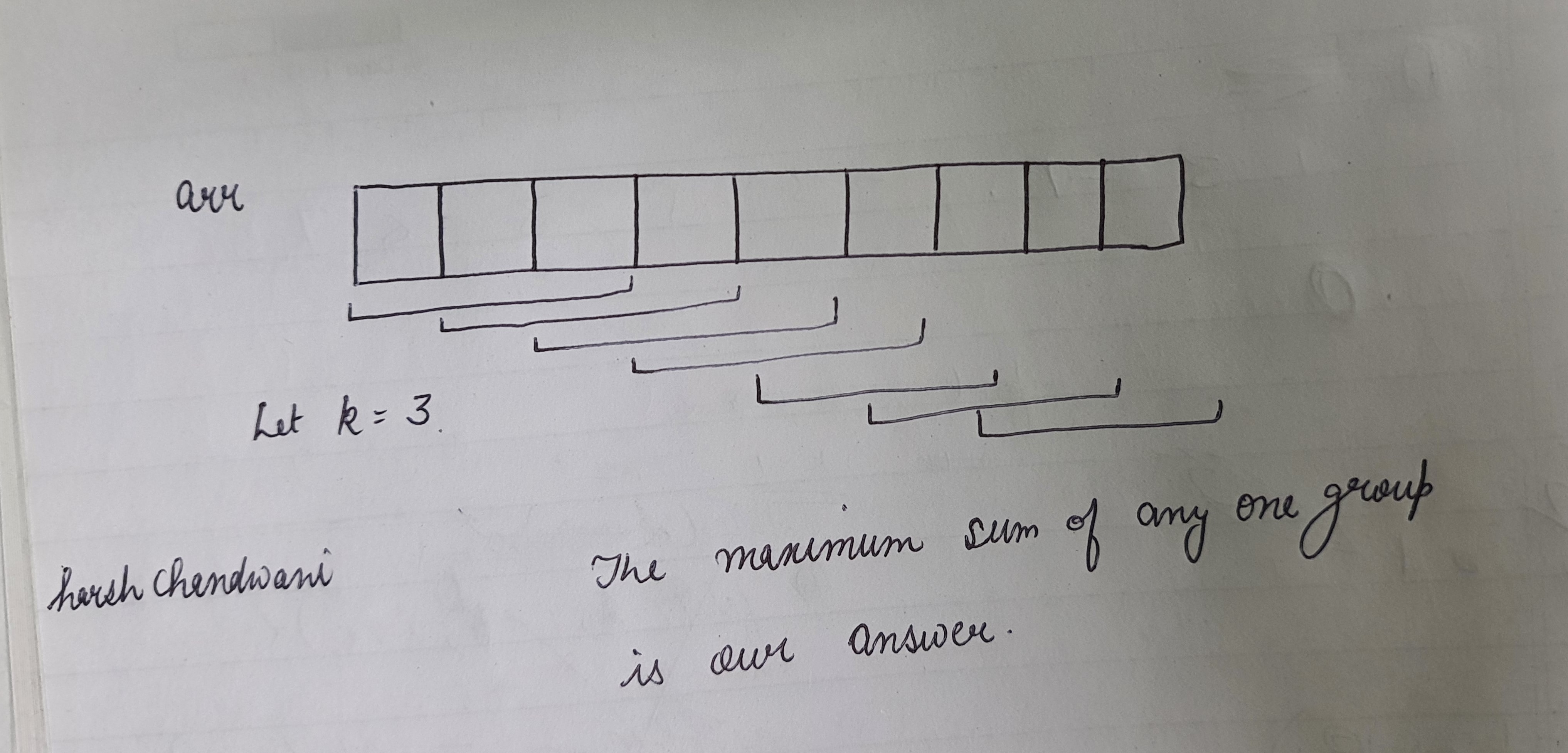
Input: Array: 14 6 2 1 5 3 7 3 K = 3

Output: 22 9 8 9 15 13 Max is 22

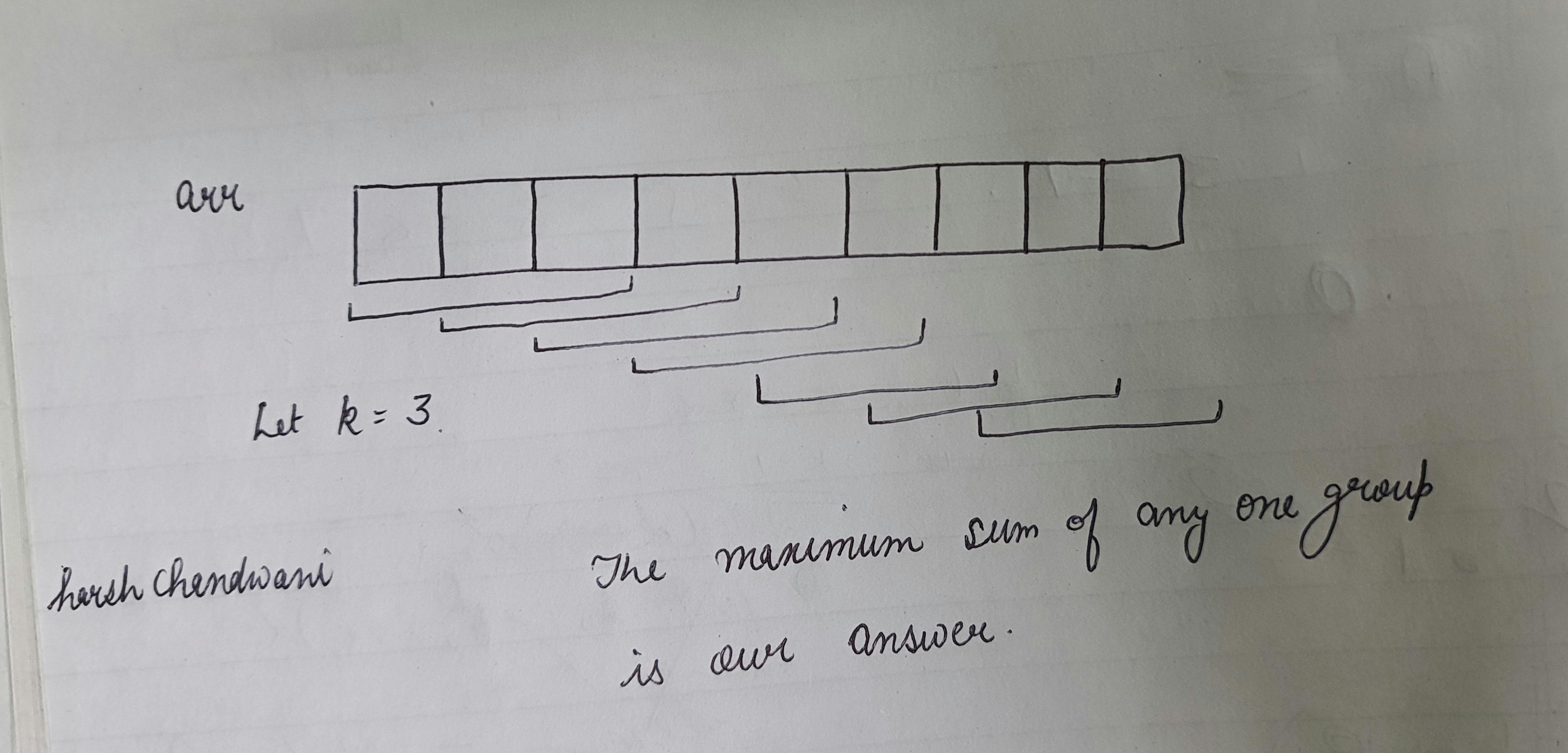
So, to solve this question and get the desired output, one way is to run a for loop till n and run another for loop till k to get the max

Solution 1:

int SlidingWindow(vector<int>& nums, int k) {
    int maxi = INT_MIN;
    for(int i=0;i<nums.size()-k+1;i++){
         int sum = 0;
          for(int j = i;j<i+k;j++){
             sum += nums[j] ;
          }
          maxi = max(maxi, sum);  
    }
    return maxi;
    }

Time Complexity: O(n*k

)

But this solution may work on some compilers and will give you answers for many test cases but this solution will give you an error called Time LimitExceed because it runs extra for loop which is not needed.

So, to solve this question we have to think of a different approach.

Let's read the question once and try to solve it for one test case. You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

Return the maximum sum from all windows.

Input: Array: 14 6 2 1 5 3 7 3 K = 3

Output: 22 9 8 9 15 13 Max is 22

So, for i = 0; We will be analyzing 3 numbers: 14 6 2 Their sum is 14 + 6 + 2 = 22

Same for i =1; Then we will analyze the next 3 numbers: 6 2 1 Their sum is 6 + 2 + 1 = 9

Did you see a pattern? When we are moving from i = 0 to i = 1 We are keeping 2 out of 3 numbers the same For i = 0: 14 6 2 For i = 1: 6 2 1

Here 6 and 2 are the same and one number is changing from 14 to 1 So can we say, while moving from i = 0 to i = 1 if we delete the first number and add the next number, we can reduce the time complexity? Yes, we can do this,

What are we doing actually: i = 0: 14 + 6 + 2 = 22 i = 1: 22 - 14 + 1 = 9

Let's implement this using code:

int SlidingWindow(int arr[], int n, int k)
{

    if (n < k)
    {
       cout << "Invalid";
       return -1;
    }


    int res = 0;
    for (int i=0; i<k; i++)
       res += arr[i];
    int curr_sum = res;
    for (int i=k; i<n; i++)
    {
       curr_sum += arr[i] - arr[i-k];
       res = max(res, curr_sum);
    }

    return res;
}

Time Complexity: O(n)

We reduced the time complexity from O(n*k) to O(n) That's what Sliding Window is Capable of.

Hope you understand what Sliding Window is, but the best way you can learn any algorithm is to practice. So, here are some questions to master Sliding Window.

LeetCode Questions

You can connect with me:

Twitter: twitter.com/heyy_harshh

LinkedIn: linkedin.com/in/harsh-chandwani